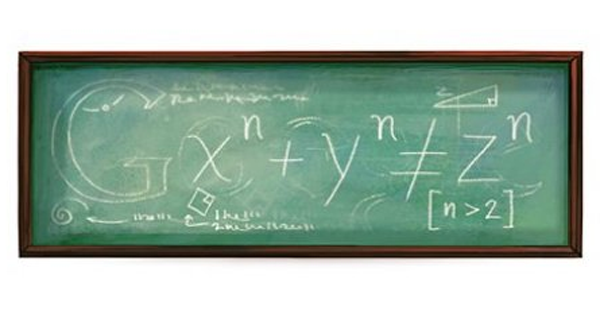A Conjectura de Beal assenta nos pressupostos do “Último Teorema de Fermat”, um desafio matemático com mais de 350 anos e que só foi provado em 1995 pelo britânico Andrew Wiles.
O problema de Beal tem despertado a curiosidade de matemáticos nos últimos 20 anos. O próprio Andrew Beal, apaixonado pela matemática, tem tentado encontrar a prova, inclusive através de sistemas de programação que o próprio desenvolveu em conjunto com um colega.
Já em 1997 este banqueiro norte-americano tinha oferecido um prémio de 378 mil euros a quem conseguisse resolver o problema. Mas uma vez que, até agora, ninguém encontrou a solução, Beal decidiu reforçar o desafio.
O objetivo é “inspirar as mentes jovens a refletir sobre a questão e torná-las mais interessadas no estudo da matemática”, afirma o milionário citado pela American Mathmatical Society em comunicado de imprensa.
Andrew Beal é um milionário do Texas que ocupa o 43º lugar da lista dos mais ricos dos Estados Unidos, da revista americana Forbes, com uma fortuna avaliada em mais de 8 mil milhões de dólares.
Saiba mais sobre este desafio AQUI.
[Notícia alterada a 08/06/2013 para acrescentar e corrigir informação sobre a Conjectura de Beal]